不的
0%

15数码问题

发表于 分类于 Disqus：

中山大学计算机学院

人工智能

本科生实验报告

**（2022学年春季学期） **

课程名称：Artificial Intelligence

一、实验题目

​ 利用A*算法以及IDA*算法实现15数码问题的求解

二、实验内容

1.算法原理

​ Astar: 从起始状态开始，把其当成待拓展状态存入一个“开启列表”，每次选取列表中未进行拓展的状态中估价函数最小的状态进行拓展，而后将它从开启列表中删除，添加到“关闭列表”中，不断搜索新的可达状态并计算它们的估价函数值，或更新待进行拓展的状态的g(x)，对已进行拓展的状态进行剪枝，直到找到目标状态或者开启列表为空。

​ IDAstar: 对估价函数值的阈值进行迭代，在迭代的每一步对于指定阙值都进行定义递归过程以进行深度优先搜索，优先选择相邻状态中估价函数值最小的状态进行递归，若当前状态的估价函数值大于当前的阈值，则进行剪枝，直到到达目标状态或无解，否则更新阈值继续迭代。

2.伪代码

Astar：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
init open[],close[]；
open[0] = start；
if open is not empty:
	choose n from open_set and f(n) has max f：
    if n == goal：
        add n to route；
        break;
    if n != goal：
        remove n from open;
		add n to close；
        find n all children：
        put children to a priorityqueue
        while queue not empty:
			pop m;
            if m in close：
                continue;
            if m not in open：
                set fathre[m] = n;
                put m to open;

IDAstar:

递归函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def IDAsearch(g, bound):
    find n in the end of the current route;
    fx = g + judge(node)
    if fx > bound:  
        return fx
    if node == goal:  
        tell main() find the goal
    mymin = ∞
    for m in children:
        if m in HISTORY:
            continue
        add m to route and route;
        t = IDAsearch(g + 1, bound)
        if t < mymin:
            mymin = t
        take out m from route and History to cancel updating
    return mymin

递归调用：

1
2
3
4
5
6
while (1):
    ans = IDAsearch(0, bound)  # g
    if (ans == 0):
        break
    bound = ans
    print(bound)
3.关键代码展示

Astar:

1
2
3
4
5
6
7
8
9
10
def judge(mat):                             # 采用曼哈顿距离来计算h(n)函数
    h = 0
    mat = list(mat)
    for i in range(4):
        for j in range(4):
            if mat[i][j] != i*4 + (j+1) and mat[i][j] != 0:
                endx = int((mat[i][j]-1)/4)
                endy = mat[i][j] - 4*endx - 1
                h = h + (abs(endx - i) + abs(endy-j))
    return h

上述代码展示的是基于列表的曼哈顿距离形式的启发式函数的相应计算，通过累加各个数字的最终位置和当前位置之间的双轴绝对值距离来得到这一启发式函数。需要注意的是不能累加时计算 0 的当前位置和最终位置之间的曼哈顿距离，因为若是累加进去的话该启发式函数将失去其可采纳性。

1
2
3
4
5
6
7
8
9
10
while not q.empty():
    fx, a, find = q.get()					# 返回的依次为fx,曼哈顿估计,局面状态
    g = fx - a
    myhash = hash(str(find))
    if myhash not in history:
        history.add(myhash)					# 加入标记走过的集合中
    if find == goal:
        print('FIND')
        break
    update(find, g)							# 探索当前局面子局面

该部分代码为A*搜索的循环体部分，通过一个优先队列的数据结构极为方便的取得优先级最高的元素，并且利用返回值获得其各项属性，利用哈希函数与集合数据结构的结合，可以明显的更为高效的判定元素是否属于集合中以进行环检测。若找到解则终止跳出，若没有则探索当前优先级最高的局面的子局面。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def update(mat, g):                                 # 找到mat可能的所有更新状态
    i = 0
    for i in range(4):
        if 0 in mat[i]:
            zeroy = i
            zeroposition = mat[i].index(0)
    zerox = zeroposition                            # 找到当前的0所在的x,y坐标
    movemat1 = copy.deepcopy(mat)
    if zeroy != 0:                                  # 以下为四个边界的判定与0的移动
        temp1 = movemat1[zeroy][zerox]
        movemat1[zeroy][zerox] = movemat1[zeroy - 1][zerox]
        movemat1[zeroy - 1][zerox] = temp1
        myhash = hash(str(movemat1))
        if myhash not in history:
            if myhash not in Open:                  # 不在开启列表中直接更新
                father[myhash] = mat
                shoot[myhash] = g + 1 + judge(movemat1)
                Open.add(myhash)
            if myhash in Open and g + 1 + judge(movemat1) < shoot[myhash]:      # 在开启列表中但是当前的父节点比先前该状态的父节点更优
                father[myhash] = mat
                shoot[myhash] = g + 1 + judge(movemat1)
            q.put([g + 1 + judge(movemat1), judge(movemat1), movemat1])         # 将fx,hx,局面放入优先队列

此函数为产生子局面的函数，由于只是为了说明，为避免附上来的代码冗长，这次选取一个移动方向进行说明。首先我们先找到 0 所在的x坐标以及y坐标，找到之后进行边界判定，并通过一个新的深拷贝的列表实现移动以及存储。

一开始我没有设计开启列表，所以在某些PPT中的案例里失去了最优性，后面通过将子节点加入开启列表并利用了设计的一个shoot字典以及father字典的组合，其中shoot字典用于存储每个局面在当前父局面的 fx 值，而father字典存储了每个局面的最优父局面，保证了每个局面都能找到它的最优父局面以及它现在的最优fx值。而之后我们通过利用father元组以及栈数据结构的组合则可以进行更加方便的输出。

1
2
3
4
5
6
7
8
light = goal
count = 0
while(1):
    S.append(light)
    if hash(str(light)) in father.keys():
        light = father[hash(str(light))]
    else:
        break

如先前所说，我们在该部分利用father元组以及栈数据结构的组合则可以在后面进行更加方便的输出，避免了在搜索时存储输出路径的步骤。

IDAstar:

1
2
3
4
5
6
7
8
9
10
def judge(state):
    h = 0
    for i in range(16):
        if state[i] != goal[i] and state[i] != 0:
            standx = i // 4
            standy = i % 4
            x = (state[i] - 1) // 4
            y = state[i] - 4*x - 1
            h = h + abs(x - standx) + abs(y - standy)
    return h

上述代码展示的是基于元组的曼哈顿距离形式的启发式函数的相应计算，通过累加各个数字的最终位置和当前位置之间的双轴绝对值距离来得到这一启发式函数。需要注意的是不能累加时计算 0 的当前位置和最终位置之间的曼哈顿距离，因为若是累加进去的话该启发式函数将失去其可采纳性。

1
2
3
4
5
6
7
8
bound = judge(start)  # IDA*迭代限制
ROUTE = [start]  # 路径集合, 视为栈
HISTORY.add(start)
while (1):
    ans = IDAsearch(0, bound)  # g, bound, 利用返回值判断递归结果
    if (ans == 0):
        break
    bound = ans

上述代码为调用递归函数的部分，首先需要初始化IDA*的界限、路径以及为了高效进行路经检测开设的集合。随后进入循环体中递归调用IDAsearch这一递归函数，并检测每次总递归的返回值，若是为 0 则表示已经找到路径可以直接终止，否则返回的就是需要更新的界限值，从而对界限值进行相应的更新。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
def IDAsearch(g, bound):
    node = ROUTE[-1]        # 找到当前路径的最后一步
    fx = g + judge(node)
    if fx > bound:       # 标记可能的阙值更新
        return fx
    if node == goal:     # 找到目标一路以0返回
        return 0

    mymin = 9999                # 用于找到该轮最小的溢出的更新值
    findzero = node.index(0)  # 寻找数码矩阵上0的坐标
    moves = []                  # 标记可移动方式
    children = []               # 存放所有子状态
    ccoo = []                   # 深拷贝当前状态以便产生儿子
    l = list(node)
    if findzero % 4 > 0:			# 4重边界判定
        ccoo = copy.deepcopy(l)
        ccoo[findzero] = ccoo[findzero - 1]
        ccoo[findzero - 1] = 0
        ccoo = tuple(ccoo)
        children.append(ccoo)
    if findzero % 4 < 3:
        ccoo = copy.deepcopy(l)
        ccoo[findzero] = ccoo[findzero + 1]
        ccoo[findzero + 1] = 0
        ccoo = tuple(ccoo)
        children.append(ccoo)
    if findzero // 4 > 0:
        ccoo = copy.deepcopy(l)
        ccoo[findzero] = ccoo[findzero - 4]
        ccoo[findzero - 4] = 0
        ccoo = tuple(ccoo)
        children.append(ccoo)
    if findzero // 4 < 3:
        ccoo = copy.deepcopy(l)
        ccoo[findzero] = ccoo[findzero + 4]
        ccoo[findzero + 4] = 0
        ccoo = tuple(ccoo)
        children.append(ccoo)

    for state in children[:]:
        if state in HISTORY:
            continue
        ROUTE.append(state)
        HISTORY.add(state)
        t = IDAsearch(g + 1, bound)         # 递归向后搜索

        if t == 0:
            return 0			# 找到目标一路以0返回
        if t < mymin:
            mymin = t

        ROUTE.pop()  # 回溯
        HISTORY.remove(state)   # 回溯
    return mymin

上述代码即为递归函数主体部分，首先找到路径走到的这最后一步，判断是否需要剪枝或者终止，若是需要就进行相应的返回，若是不需要就找到其相应的子节点，并以这些子节点为新的基准开始递归调用，调用结束后首先判0以便于找到相应目标时进行一路返回，若是还是没找到就找到一个最小更新阙值 (mymin) 进行阙值的更新，然后进行回溯即可。

4.思考与创新点

分别对列表以及元组形式的存储方式都进行了尝试，但是由于列表虽然表面上是不可哈希的，实际上却通过将其转化为字符串形式再求哈希所以对于环检测和路经检测来说二者之间效率区别不明显。

另外也尝试了采用 fx = g + 1.01*h 代替 fx = g + h 来构建新的启发式函数欲提高效率，然而实际上尝试了之后发现时间上也并没有明显的节省。

最重要的还是对于A*算法进行环检测以及对IDA*算法进行路经检测，显然检测的手段是判断是否有先前的某个元素，而对于这种判断最高效的结构就是集合数据结构，若是采用列表需要将列表转为字符串然后进行哈希再存入集合中，若是使用元组可以直接存入集合中，而后利用是否在集合中的判断相比于没有使用集合数据结构就可以明显高效的进行环检测和路经检测。

在A*部分中我尝试在搜索中不保存输出路径，避免长期维持输出路径带来的时间空间上的开销，而只是保存每个局面的父局面，最后搜索完毕后再利用栈数据结构往回入栈，从而得到了一条路径以便之后进行输出。

由于我们采用启发式函数构造的 fx 很有可能相同，导致以课上所讲的方法很难在 fx 相同的情况下挑出一条更优的局面，只会在 fx 相同的各个局面里随机挑选，严重影响了搜索的效率，所以在实验中，我尝试利用两重优先级的优先队列，第一个优先级为 fx ，第二个优先级为 hx ，由于 hx 小实际上也一定程度上标志了距离目标的距离小，所以这种构造方法也是具有合理性的。经过实际的尝试该方法的确明显降低了搜索所需要的时间。

三、实验结果及分析

1.实验结果展示示例

各个结果已经作为文件存储到文件夹中，各结果详情烦请帮我们批改师兄师姐查阅。

结果分析要求

(1) 对比分析A*和IDA*的性能和结果

理论上来说，IDA*在处理更加复杂的局面时应该优于A*，然而实际上在该实验中给出的8个局面中经过优化的A*算法都比IDA*跑的更快。不过在 github 上搜索到一些大佬优化IDA*算法的程序，比如说选用了 walking distance 启发式函数等，的确在更加复杂的问题中就能够明显优于经过优化的A*算法了。

下述为选取的一些例子：

PPT第二个：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
ROUND 0:
[[14, 10, 6, 0], [4, 9, 1, 8], [2, 3, 5, 11], [12, 13, 7, 15]]
ROUND 1:
[[14, 10, 0, 6], [4, 9, 1, 8], [2, 3, 5, 11], [12, 13, 7, 15]]
ROUND 2:
[[14, 0, 10, 6], [4, 9, 1, 8], [2, 3, 5, 11], [12, 13, 7, 15]]
ROUND 3:
[[14, 9, 10, 6], [4, 0, 1, 8], [2, 3, 5, 11], [12, 13, 7, 15]]
ROUND 4:
[[14, 9, 10, 6], [0, 4, 1, 8], [2, 3, 5, 11], [12, 13, 7, 15]]
ROUND 5:
[[0, 9, 10, 6], [14, 4, 1, 8], [2, 3, 5, 11], [12, 13, 7, 15]]
ROUND 6:
[[9, 0, 10, 6], [14, 4, 1, 8], [2, 3, 5, 11], [12, 13, 7, 15]]
ROUND 7:
[[9, 4, 10, 6], [14, 0, 1, 8], [2, 3, 5, 11], [12, 13, 7, 15]]
ROUND 8:
[[9, 4, 10, 6], [14, 1, 0, 8], [2, 3, 5, 11], [12, 13, 7, 15]]
ROUND 9:
[[9, 4, 0, 6], [14, 1, 10, 8], [2, 3, 5, 11], [12, 13, 7, 15]]
ROUND 10:
[[9, 0, 4, 6], [14, 1, 10, 8], [2, 3, 5, 11], [12, 13, 7, 15]]
ROUND 11:
[[9, 1, 4, 6], [14, 0, 10, 8], [2, 3, 5, 11], [12, 13, 7, 15]]
ROUND 12:
[[9, 1, 4, 6], [14, 3, 10, 8], [2, 0, 5, 11], [12, 13, 7, 15]]
ROUND 13:
[[9, 1, 4, 6], [14, 3, 10, 8], [0, 2, 5, 11], [12, 13, 7, 15]]
ROUND 14:
[[9, 1, 4, 6], [0, 3, 10, 8], [14, 2, 5, 11], [12, 13, 7, 15]]
ROUND 15:
[[0, 1, 4, 6], [9, 3, 10, 8], [14, 2, 5, 11], [12, 13, 7, 15]]
ROUND 16:
[[1, 0, 4, 6], [9, 3, 10, 8], [14, 2, 5, 11], [12, 13, 7, 15]]
ROUND 17:
[[1, 3, 4, 6], [9, 0, 10, 8], [14, 2, 5, 11], [12, 13, 7, 15]]
ROUND 18:
[[1, 3, 4, 6], [9, 2, 10, 8], [14, 0, 5, 11], [12, 13, 7, 15]]
ROUND 19:
[[1, 3, 4, 6], [9, 2, 10, 8], [14, 5, 0, 11], [12, 13, 7, 15]]
ROUND 20:
[[1, 3, 4, 6], [9, 2, 10, 8], [14, 5, 11, 0], [12, 13, 7, 15]]
ROUND 21:
[[1, 3, 4, 6], [9, 2, 10, 0], [14, 5, 11, 8], [12, 13, 7, 15]]
ROUND 22:
[[1, 3, 4, 0], [9, 2, 10, 6], [14, 5, 11, 8], [12, 13, 7, 15]]
ROUND 23:
[[1, 3, 0, 4], [9, 2, 10, 6], [14, 5, 11, 8], [12, 13, 7, 15]]
ROUND 24:
[[1, 0, 3, 4], [9, 2, 10, 6], [14, 5, 11, 8], [12, 13, 7, 15]]
ROUND 25:
[[1, 2, 3, 4], [9, 0, 10, 6], [14, 5, 11, 8], [12, 13, 7, 15]]
ROUND 26:
[[1, 2, 3, 4], [9, 5, 10, 6], [14, 0, 11, 8], [12, 13, 7, 15]]
ROUND 27:
[[1, 2, 3, 4], [9, 5, 10, 6], [14, 13, 11, 8], [12, 0, 7, 15]]
ROUND 28:
[[1, 2, 3, 4], [9, 5, 10, 6], [14, 13, 11, 8], [0, 12, 7, 15]]
ROUND 29:
[[1, 2, 3, 4], [9, 5, 10, 6], [0, 13, 11, 8], [14, 12, 7, 15]]
ROUND 30:
[[1, 2, 3, 4], [9, 5, 10, 6], [13, 0, 11, 8], [14, 12, 7, 15]]
ROUND 31:
[[1, 2, 3, 4], [9, 5, 10, 6], [13, 12, 11, 8], [14, 0, 7, 15]]
ROUND 32:
[[1, 2, 3, 4], [9, 5, 10, 6], [13, 12, 11, 8], [14, 7, 0, 15]]
ROUND 33:
[[1, 2, 3, 4], [9, 5, 10, 6], [13, 12, 0, 8], [14, 7, 11, 15]]
ROUND 34:
[[1, 2, 3, 4], [9, 5, 10, 6], [13, 0, 12, 8], [14, 7, 11, 15]]
ROUND 35:
[[1, 2, 3, 4], [9, 5, 10, 6], [13, 7, 12, 8], [14, 0, 11, 15]]
ROUND 36:
[[1, 2, 3, 4], [9, 5, 10, 6], [13, 7, 12, 8], [0, 14, 11, 15]]
ROUND 37:
[[1, 2, 3, 4], [9, 5, 10, 6], [0, 7, 12, 8], [13, 14, 11, 15]]
ROUND 38:
[[1, 2, 3, 4], [0, 5, 10, 6], [9, 7, 12, 8], [13, 14, 11, 15]]
ROUND 39:
[[1, 2, 3, 4], [5, 0, 10, 6], [9, 7, 12, 8], [13, 14, 11, 15]]
ROUND 40:
[[1, 2, 3, 4], [5, 10, 0, 6], [9, 7, 12, 8], [13, 14, 11, 15]]
ROUND 41:
[[1, 2, 3, 4], [5, 10, 6, 0], [9, 7, 12, 8], [13, 14, 11, 15]]
ROUND 42:
[[1, 2, 3, 4], [5, 10, 6, 8], [9, 7, 12, 0], [13, 14, 11, 15]]
ROUND 43:
[[1, 2, 3, 4], [5, 10, 6, 8], [9, 7, 0, 12], [13, 14, 11, 15]]
ROUND 44:
[[1, 2, 3, 4], [5, 10, 6, 8], [9, 0, 7, 12], [13, 14, 11, 15]]
ROUND 45:
[[1, 2, 3, 4], [5, 0, 6, 8], [9, 10, 7, 12], [13, 14, 11, 15]]
ROUND 46:
[[1, 2, 3, 4], [5, 6, 0, 8], [9, 10, 7, 12], [13, 14, 11, 15]]
ROUND 47:
[[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 0, 12], [13, 14, 11, 15]]
ROUND 48:
[[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 0, 15]]
ROUND 49:
[[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 0]]
STEPS: 49
Running time: 48.318987899999996 Seconds
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
ROUND: 0
14 10 6 0 
4 9 1 8 
2 3 5 11 
12 13 7 15 

ROUND: 1
14 10 0 6 
4 9 1 8 
2 3 5 11 
12 13 7 15 

ROUND: 2
14 0 10 6 
4 9 1 8 
2 3 5 11 
12 13 7 15 

ROUND: 3
14 9 10 6 
4 0 1 8 
2 3 5 11 
12 13 7 15 

ROUND: 4
14 9 10 6 
0 4 1 8 
2 3 5 11 
12 13 7 15 

ROUND: 5
0 9 10 6 
14 4 1 8 
2 3 5 11 
12 13 7 15 

ROUND: 6
9 0 10 6 
14 4 1 8 
2 3 5 11 
12 13 7 15 

ROUND: 7
9 4 10 6 
14 0 1 8 
2 3 5 11 
12 13 7 15 

ROUND: 8
9 4 10 6 
14 1 0 8 
2 3 5 11 
12 13 7 15 

ROUND: 9
9 4 0 6 
14 1 10 8 
2 3 5 11 
12 13 7 15 

ROUND: 10
9 0 4 6 
14 1 10 8 
2 3 5 11 
12 13 7 15 

ROUND: 11
9 1 4 6 
14 0 10 8 
2 3 5 11 
12 13 7 15 

ROUND: 12
9 1 4 6 
14 3 10 8 
2 0 5 11 
12 13 7 15 

ROUND: 13
9 1 4 6 
14 3 10 8 
0 2 5 11 
12 13 7 15 

ROUND: 14
9 1 4 6 
0 3 10 8 
14 2 5 11 
12 13 7 15 

ROUND: 15
0 1 4 6 
9 3 10 8 
14 2 5 11 
12 13 7 15 

ROUND: 16
1 0 4 6 
9 3 10 8 
14 2 5 11 
12 13 7 15 

ROUND: 17
1 3 4 6 
9 0 10 8 
14 2 5 11 
12 13 7 15 

ROUND: 18
1 3 4 6 
9 2 10 8 
14 0 5 11 
12 13 7 15 

ROUND: 19
1 3 4 6 
9 2 10 8 
14 5 0 11 
12 13 7 15 

ROUND: 20
1 3 4 6 
9 2 10 8 
14 5 11 0 
12 13 7 15 

ROUND: 21
1 3 4 6 
9 2 10 0 
14 5 11 8 
12 13 7 15 

ROUND: 22
1 3 4 0 
9 2 10 6 
14 5 11 8 
12 13 7 15 

ROUND: 23
1 3 0 4 
9 2 10 6 
14 5 11 8 
12 13 7 15 

ROUND: 24
1 0 3 4 
9 2 10 6 
14 5 11 8 
12 13 7 15 

ROUND: 25
1 2 3 4 
9 0 10 6 
14 5 11 8 
12 13 7 15 

ROUND: 26
1 2 3 4 
9 5 10 6 
14 0 11 8 
12 13 7 15 

ROUND: 27
1 2 3 4 
9 5 10 6 
14 13 11 8 
12 0 7 15 

ROUND: 28
1 2 3 4 
9 5 10 6 
14 13 11 8 
0 12 7 15 

ROUND: 29
1 2 3 4 
9 5 10 6 
0 13 11 8 
14 12 7 15 

ROUND: 30
1 2 3 4 
9 5 10 6 
13 0 11 8 
14 12 7 15 

ROUND: 31
1 2 3 4 
9 5 10 6 
13 12 11 8 
14 0 7 15 

ROUND: 32
1 2 3 4 
9 5 10 6 
13 12 11 8 
14 7 0 15 

ROUND: 33
1 2 3 4 
9 5 10 6 
13 12 0 8 
14 7 11 15 

ROUND: 34
1 2 3 4 
9 5 10 6 
13 0 12 8 
14 7 11 15 

ROUND: 35
1 2 3 4 
9 5 10 6 
13 7 12 8 
14 0 11 15 

ROUND: 36
1 2 3 4 
9 5 10 6 
13 7 12 8 
0 14 11 15 

ROUND: 37
1 2 3 4 
9 5 10 6 
0 7 12 8 
13 14 11 15 

ROUND: 38
1 2 3 4 
0 5 10 6 
9 7 12 8 
13 14 11 15 

ROUND: 39
1 2 3 4 
5 0 10 6 
9 7 12 8 
13 14 11 15 

ROUND: 40
1 2 3 4 
5 10 0 6 
9 7 12 8 
13 14 11 15 

ROUND: 41
1 2 3 4 
5 10 6 0 
9 7 12 8 
13 14 11 15 

ROUND: 42
1 2 3 4 
5 10 6 8 
9 7 12 0 
13 14 11 15 

ROUND: 43
1 2 3 4 
5 10 6 8 
9 7 0 12 
13 14 11 15 

ROUND: 44
1 2 3 4 
5 10 6 8 
9 0 7 12 
13 14 11 15 

ROUND: 45
1 2 3 4 
5 0 6 8 
9 10 7 12 
13 14 11 15 

ROUND: 46
1 2 3 4 
5 6 0 8 
9 10 7 12 
13 14 11 15 

ROUND: 47
1 2 3 4 
5 6 7 8 
9 10 0 12 
13 14 11 15 

ROUND: 48
1 2 3 4 
5 6 7 8 
9 10 11 12 
13 14 0 15 

ROUND: 49
1 2 3 4 
5 6 7 8 
9 10 11 12 
13 14 15 0 

Total 49
TIME EXPENDED 62.636021

压缩包第二个：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
ROUND 0:
[[1, 7, 8, 10], [6, 9, 15, 14], [13, 3, 0, 4], [11, 5, 12, 2]]
ROUND 1:
[[1, 7, 8, 10], [6, 9, 0, 14], [13, 3, 15, 4], [11, 5, 12, 2]]
ROUND 2:
[[1, 7, 8, 10], [6, 9, 14, 0], [13, 3, 15, 4], [11, 5, 12, 2]]
ROUND 3:
[[1, 7, 8, 10], [6, 9, 14, 4], [13, 3, 15, 0], [11, 5, 12, 2]]
ROUND 4:
[[1, 7, 8, 10], [6, 9, 14, 4], [13, 3, 15, 2], [11, 5, 12, 0]]
ROUND 5:
[[1, 7, 8, 10], [6, 9, 14, 4], [13, 3, 15, 2], [11, 5, 0, 12]]
ROUND 6:
[[1, 7, 8, 10], [6, 9, 14, 4], [13, 3, 0, 2], [11, 5, 15, 12]]
ROUND 7:
[[1, 7, 8, 10], [6, 9, 0, 4], [13, 3, 14, 2], [11, 5, 15, 12]]
ROUND 8:
[[1, 7, 0, 10], [6, 9, 8, 4], [13, 3, 14, 2], [11, 5, 15, 12]]
ROUND 9:
[[1, 7, 10, 0], [6, 9, 8, 4], [13, 3, 14, 2], [11, 5, 15, 12]]
ROUND 10:
[[1, 7, 10, 4], [6, 9, 8, 0], [13, 3, 14, 2], [11, 5, 15, 12]]
ROUND 11:
[[1, 7, 10, 4], [6, 9, 0, 8], [13, 3, 14, 2], [11, 5, 15, 12]]
ROUND 12:
[[1, 7, 10, 4], [6, 0, 9, 8], [13, 3, 14, 2], [11, 5, 15, 12]]
ROUND 13:
[[1, 7, 10, 4], [6, 3, 9, 8], [13, 0, 14, 2], [11, 5, 15, 12]]
ROUND 14:
[[1, 7, 10, 4], [6, 3, 9, 8], [13, 5, 14, 2], [11, 0, 15, 12]]
ROUND 15:
[[1, 7, 10, 4], [6, 3, 9, 8], [13, 5, 14, 2], [0, 11, 15, 12]]
ROUND 16:
[[1, 7, 10, 4], [6, 3, 9, 8], [0, 5, 14, 2], [13, 11, 15, 12]]
ROUND 17:
[[1, 7, 10, 4], [6, 3, 9, 8], [5, 0, 14, 2], [13, 11, 15, 12]]
ROUND 18:
[[1, 7, 10, 4], [6, 3, 9, 8], [5, 14, 0, 2], [13, 11, 15, 12]]
ROUND 19:
[[1, 7, 10, 4], [6, 3, 9, 8], [5, 14, 2, 0], [13, 11, 15, 12]]
ROUND 20:
[[1, 7, 10, 4], [6, 3, 9, 8], [5, 14, 2, 12], [13, 11, 15, 0]]
ROUND 21:
[[1, 7, 10, 4], [6, 3, 9, 8], [5, 14, 2, 12], [13, 11, 0, 15]]
ROUND 22:
[[1, 7, 10, 4], [6, 3, 9, 8], [5, 14, 2, 12], [13, 0, 11, 15]]
ROUND 23:
[[1, 7, 10, 4], [6, 3, 9, 8], [5, 0, 2, 12], [13, 14, 11, 15]]
ROUND 24:
[[1, 7, 10, 4], [6, 3, 9, 8], [5, 2, 0, 12], [13, 14, 11, 15]]
ROUND 25:
[[1, 7, 10, 4], [6, 3, 0, 8], [5, 2, 9, 12], [13, 14, 11, 15]]
ROUND 26:
[[1, 7, 0, 4], [6, 3, 10, 8], [5, 2, 9, 12], [13, 14, 11, 15]]
ROUND 27:
[[1, 0, 7, 4], [6, 3, 10, 8], [5, 2, 9, 12], [13, 14, 11, 15]]
ROUND 28:
[[1, 3, 7, 4], [6, 0, 10, 8], [5, 2, 9, 12], [13, 14, 11, 15]]
ROUND 29:
[[1, 3, 7, 4], [6, 2, 10, 8], [5, 0, 9, 12], [13, 14, 11, 15]]
ROUND 30:
[[1, 3, 7, 4], [6, 2, 10, 8], [5, 9, 0, 12], [13, 14, 11, 15]]
ROUND 31:
[[1, 3, 7, 4], [6, 2, 0, 8], [5, 9, 10, 12], [13, 14, 11, 15]]
ROUND 32:
[[1, 3, 0, 4], [6, 2, 7, 8], [5, 9, 10, 12], [13, 14, 11, 15]]
ROUND 33:
[[1, 0, 3, 4], [6, 2, 7, 8], [5, 9, 10, 12], [13, 14, 11, 15]]
ROUND 34:
[[1, 2, 3, 4], [6, 0, 7, 8], [5, 9, 10, 12], [13, 14, 11, 15]]
ROUND 35:
[[1, 2, 3, 4], [0, 6, 7, 8], [5, 9, 10, 12], [13, 14, 11, 15]]
ROUND 36:
[[1, 2, 3, 4], [5, 6, 7, 8], [0, 9, 10, 12], [13, 14, 11, 15]]
ROUND 37:
[[1, 2, 3, 4], [5, 6, 7, 8], [9, 0, 10, 12], [13, 14, 11, 15]]
ROUND 38:
[[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 0, 12], [13, 14, 11, 15]]
ROUND 39:
[[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 0, 15]]
ROUND 40:
[[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 0]]
STEPS: 40
Running time: 0.14140119999999998 Seconds
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
ROUND: 0
1 7 8 10 
6 9 15 14 
13 3 0 4 
11 5 12 2 

ROUND: 1
1 7 8 10 
6 9 0 14 
13 3 15 4 
11 5 12 2 

ROUND: 2
1 7 8 10 
6 9 14 0 
13 3 15 4 
11 5 12 2 

ROUND: 3
1 7 8 10 
6 9 14 4 
13 3 15 0 
11 5 12 2 

ROUND: 4
1 7 8 10 
6 9 14 4 
13 3 0 15 
11 5 12 2 

ROUND: 5
1 7 8 10 
6 9 0 4 
13 3 14 15 
11 5 12 2 

ROUND: 6
1 7 8 10 
6 0 9 4 
13 3 14 15 
11 5 12 2 

ROUND: 7
1 7 8 10 
6 3 9 4 
13 0 14 15 
11 5 12 2 

ROUND: 8
1 7 8 10 
6 3 9 4 
13 5 14 15 
11 0 12 2 

ROUND: 9
1 7 8 10 
6 3 9 4 
13 5 14 15 
0 11 12 2 

ROUND: 10
1 7 8 10 
6 3 9 4 
0 5 14 15 
13 11 12 2 

ROUND: 11
1 7 8 10 
6 3 9 4 
5 0 14 15 
13 11 12 2 

ROUND: 12
1 7 8 10 
6 3 9 4 
5 14 0 15 
13 11 12 2 

ROUND: 13
1 7 8 10 
6 3 9 4 
5 14 12 15 
13 11 0 2 

ROUND: 14
1 7 8 10 
6 3 9 4 
5 14 12 15 
13 11 2 0 

ROUND: 15
1 7 8 10 
6 3 9 4 
5 14 12 0 
13 11 2 15 

ROUND: 16
1 7 8 10 
6 3 9 4 
5 14 0 12 
13 11 2 15 

ROUND: 17
1 7 8 10 
6 3 9 4 
5 14 2 12 
13 11 0 15 

ROUND: 18
1 7 8 10 
6 3 9 4 
5 14 2 12 
13 0 11 15 

ROUND: 19
1 7 8 10 
6 3 9 4 
5 0 2 12 
13 14 11 15 

ROUND: 20
1 7 8 10 
6 3 9 4 
5 2 0 12 
13 14 11 15 

ROUND: 21
1 7 8 10 
6 3 0 4 
5 2 9 12 
13 14 11 15 

ROUND: 22
1 7 0 10 
6 3 8 4 
5 2 9 12 
13 14 11 15 

ROUND: 23
1 7 10 0 
6 3 8 4 
5 2 9 12 
13 14 11 15 

ROUND: 24
1 7 10 4 
6 3 8 0 
5 2 9 12 
13 14 11 15 

ROUND: 25
1 7 10 4 
6 3 0 8 
5 2 9 12 
13 14 11 15 

ROUND: 26
1 7 0 4 
6 3 10 8 
5 2 9 12 
13 14 11 15 

ROUND: 27
1 0 7 4 
6 3 10 8 
5 2 9 12 
13 14 11 15 

ROUND: 28
1 3 7 4 
6 0 10 8 
5 2 9 12 
13 14 11 15 

ROUND: 29
1 3 7 4 
6 2 10 8 
5 0 9 12 
13 14 11 15 

ROUND: 30
1 3 7 4 
6 2 10 8 
5 9 0 12 
13 14 11 15 

ROUND: 31
1 3 7 4 
6 2 0 8 
5 9 10 12 
13 14 11 15 

ROUND: 32
1 3 0 4 
6 2 7 8 
5 9 10 12 
13 14 11 15 

ROUND: 33
1 0 3 4 
6 2 7 8 
5 9 10 12 
13 14 11 15 

ROUND: 34
1 2 3 4 
6 0 7 8 
5 9 10 12 
13 14 11 15 

ROUND: 35
1 2 3 4 
0 6 7 8 
5 9 10 12 
13 14 11 15 

ROUND: 36
1 2 3 4 
5 6 7 8 
0 9 10 12 
13 14 11 15 

ROUND: 37
1 2 3 4 
5 6 7 8 
9 0 10 12 
13 14 11 15 

ROUND: 38
1 2 3 4 
5 6 7 8 
9 10 0 12 
13 14 11 15 

ROUND: 39
1 2 3 4 
5 6 7 8 
9 10 11 12 
13 14 0 15 

ROUND: 40
1 2 3 4 
5 6 7 8 
9 10 11 12 
13 14 15 0 

Total 40
TIME EXPENDED 0.192887

例如从文件中挑取的最上面两个结果为PPT的第二个例子的运行结果（PPT第一个和第三个例子用了上述优化还是跑了几节课都没跑出来）。底下的两个结果为压缩包的第二个例子的运行结果。两种起始局面下，A*算法都跑的比IDA*算法更快。且压缩包中的测试案例由于其起始局面更接近于目的局面，所以探索的比PPT中的测试案例快许多。

可以从上面的结果中看出尽管PPT第二个的搜索中结果需要走49步才能达到，A*算法的运行时间仍然优于IDA*算法的运行时间。不过A*算法领先于IDA*算法的幅度相比于更加简单的局面（诸如压缩包第二个）来说显然更少，可以推测在更加复杂的局面中，IDA*算法的效率会逐渐超过A*算法。

其实二者在这其中的一个很大的差异是A*是广度优先搜索的一种，而广度优先我们在之间的课程中可以知道空间复杂度为 O (b^d^)，并且需要维护一个优先队列，对队列的操作需要 O(log n) 的时间复杂度，随着结点数增多，维护这个队列的开销会急剧上升，同时空间复杂度的上升将比时间复杂度的上升更让我们难以接受，最终可能出现内存爆炸的问题。而IDA*则是深度优先搜索中的一种，从之前的课程中可以知道其空间复杂度为 O (bd)，虽然在刚起步的时候需要对限制值进行不停的更新，然后从头再开始搜索，但是在结点越来越多的情况下，由于其不需要维护庞大的空间，最后在效率上将能够超越A*。

附：

另外在最后的测试中，我尝试在test3.py程序中直接不更改 g 的值，也就是保持着g为 0，fx = g + hx 此时退化成了 fx = hx。这种方法失去了最优性，需要走很多步才能达到目标状态，但是找到答案的速度却异常的快，能够快速解决PPT中的所有例子。其结果我保存在了名如 ‘’resultAtest_ppt1.txt’’ 的几个文件中。

(2) 如果使用了多种启发式函数也可以进行对比和分析

以下分别对错位数码、曼哈顿距离、切比雪夫距离的压缩包例子进行了测试以及对比分析：

1
2
需要步数为:40
Running time: 0.14140119999999998 Seconds
1
2
需要步数为:40
Running time: 146.5895067 Seconds

错位数码运行时内存占用过大。

曼哈顿距离为上述的第一个结果，切比雪夫距离为上述的第三个结果，可以看到曼哈顿距离的启发式函数极其明显的快于切比雪夫距离的启发式函数，几乎是1000倍的差距。其实考虑到三个启发式函数的构造方法这其实也是较为自然的。

第一种启发式函数也就是错位数码几乎完全没有考虑数码所在空间之间的相互关系（只是单纯判断是否在目的位置上），这时候 0 在第一行第一列和在第三行第四列对于 0 的错位判断是相同的，但我们知道这操作起来的难度完全不同。

而切比雪夫距离选取横纵距离之间最大的距离参与估计，这其实相对来说也较为片面，在横纵距离之间相差不大时会较大程度的影响到判断，比如说数字4在第一行第一列和在第四行第一列对于数字4的切比雪夫距离判断是相同的，然而我们知道这两个状态距离目标的程度完全是不同的。

曼哈顿距离则较为周全的考虑了横纵距离相加和，这也有考虑到15数码问题中，数字只能上下左右移动的因素，所以相比于上述两个启发式函数时间损耗显然更加少。

然而其实在下述例子中：

1 2 3 0

5 6 7 8

9 10 11 12

13 14 15 4

我们得到曼哈顿距离启发式函数为3，但是实际上这不可能用3手就解开，可见曼哈顿函数只是着眼于自己本身以及所要达到的目标，忽略了其它数字带来的影响。

在查阅资料中，我看到一篇日文博客讨论了一个新的启发式函数——Walking distance。该方法“只着眼于上下动，看最低需要多少手”。

wd

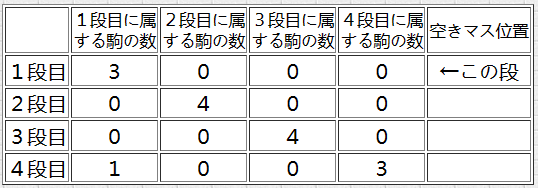
image-20230403214357128

基本思路如上图所示，忽略了左右移动，将同一水平上的数据同等对待，并且使用“从目标状态开始”的反向逆解执行搜索，将结果作为数据表保存，最后得到一个数据量只有24964种模式的数据表。参照此数据表，可以从任意状态中得到比曼哈顿距离更优的“最低限度必要的上下移动次数”（实际上也就是更接近于到目标位置的真实距离）。由于时间问题我并没有自己实践一遍这个函数，不过在github上搜索了一番是否有人用这个启发式函数发现的确有，并且跑起来明显快于曼哈顿距离的启发式函数。

四、思考题

这次实验暂未给出思考题。

五、参考资料

① week5&6 Astar & IDAstar.ppt

② UninformSearch.ppt

③１５パズル自動解答プログラムの作り方 ——computerpuzzle.net/puzzle/15puzzle/index.html