不的
0%

大学生录取预测分类训练

发表于 更新于 分类于 Disqus：

中山大学计算机学院

人工智能

本科生实验报告

（2022学年春季学期）

课程名称：Artificial Intelligence

一、实验题目

在数据集data1.txt上完成大学生录取预测分类训练：

​ 设计合适的网络结构，选择合适的损失函数

​ 利用训练集完成网络训练画出数据可视化图、loss曲线图，计算模型收敛后的分类准确率。

二、实验内容

1.算法原理

线性回归试图找到一条合适的直线y=w*x+b，让直线尽可能多的穿过样本点来拟合数据，说明特征值与标签值之间的规律。达到通过特征值来预测标签值的效果，而要找到最优的直线，需要通过不断调整权重w来实现，直到w使得所有的预测值与真实值之间的误差之和最小化，也就是损失函数（也叫代价函数）最小化。

    • 1）初始化权重w和截距b来构建最初的模型。

    • 2）使用这个模型来计算损失函数

    • 3）对损失函数求偏导

        • 损失最小时，损失函数的导数值为0。
    • 4）运用偏导值和学习率更新权重，重复2~4步

优点：

　　（1）思想简单，实现容易。建模迅速，对于小数据量、简单的关系很有效；

　　（2）是许多强大的非线性模型的基础。

　　（3）线性回归模型十分容易理解，结果具有很好的可解释性，有利于决策分析。

　　（4）蕴含机器学习中的很多重要思想。

　　（5）能解决回归问题。

缺点：

　　（1）对于非线性数据或者数据特征间具有相关性多项式回归难以建模.

　　（2）难以很好地表达高度复杂的数据。

2.关键代码展示
1
2
3
4
5
6
data = np.genfromtxt('C:\\Users\\Gabriel\\Desktop\\data1.txt', delimiter=',')
X = data[:, :-1]  # 数据向量
Y = data[:, -1]   # 标签向量

X = (X - np.mean(X, axis=0)) / np.std(X, axis=0)   # 正则化
X = np.concatenate((np.ones((X.shape[0], 1)), X), axis=1)    # 添加偏置

上面的代码用于读入txt文件，并且将数据的数据部分和标签部分分离开来以便后面的各项操作。我们还需要将得到的数据进行正则化和偏置处理，正则化可以避免过拟合，偏置则通过引入一个额外的常数提高模型的表达能力。

1
2
3
4
5
6
7
8
9
def sigmoid(x):
    return 1 / (1 + np.exp(-x))


def loss_function(X, Y, weight):
    m = len(Y)
    h = sigmoid(np.dot(X, weight))
    loss = -(1/m) * (np.dot(Y, np.log(h)) + np.dot((1-Y), np.log(1-h)))
    return loss

上面的代码定义两个函数，第一个是简单的计算sigmoid的函数。第二个是计算损失函数的函数，先通过点积加上sigmoid求出预测值h，再用预测值和真实值计算出损失函数，此处也需要按PPT上的添加上一个正则化避免过拟合。

1
2
3
4
5
6
7
8
loss_history = []           # 损失记录
for i in range(num_iterations):
    h = sigmoid(np.dot(X, weight))
    # 计算当前损失值
    loss = loss_function(X, Y, weight)
    gradient = np.dot(X.T, (-Y/h + (1 - Y)/(1 - h)) * h * (1 - h))
    weight -= learning_rate * gradient       # 更新权重
    loss_history.append(loss)

该部分代码为训练代码，我们一开始定义一个数组用于存放训练过程中的各个损失值。每次训练我们先用点积计算出预测值，随后对weight进行更新，我们通过对损失函数的求导式来更新。随后我们计算损失函数值，并添加到列表中便于之后图形的绘制。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 绘制分类图
plt.scatter(X[:, 1], X[:, 2], c=Y, cmap='bwr')
plt.xlabel('Score 1')
plt.ylabel('Score 2')
x1 = np.linspace(np.min(X[:, 1]), np.max(X[:, 1]), 100)
x2 = -(weight[0] + weight[1] * x1) / weight[2]
plt.plot(x1, x2, color='black')
plt.title('Predictions')
plt.show()


# 绘制损失曲线
plt.plot(range(num_iterations), loss_history)
plt.xlabel('Iterations')
plt.ylabel('Loss')
plt.title('Loss Curve')
plt.show()

# 计算分类准确率
predictions = np.round(sigmoid(np.dot(X, weight)))
accuracy = np.mean(predictions == Y)
print(f'分类准确率为:%.2lf ' % accuracy)

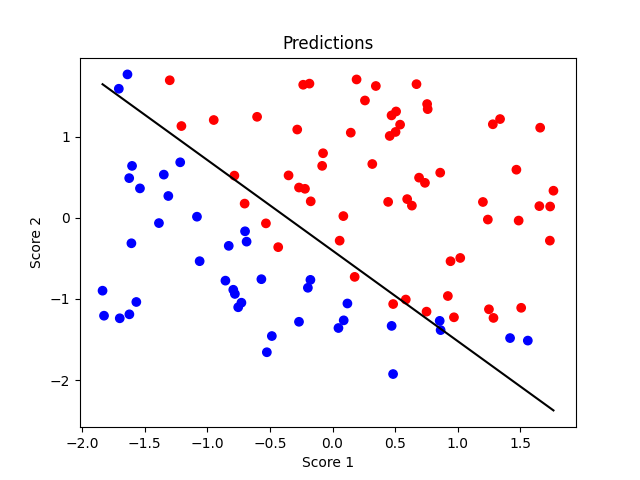
该部分代码为图形绘制部分代码，我们第一张图先画了分类图，我们通过标签对各个点进行上色，并且根据我们的回归结果画出分类界线以进行比对。

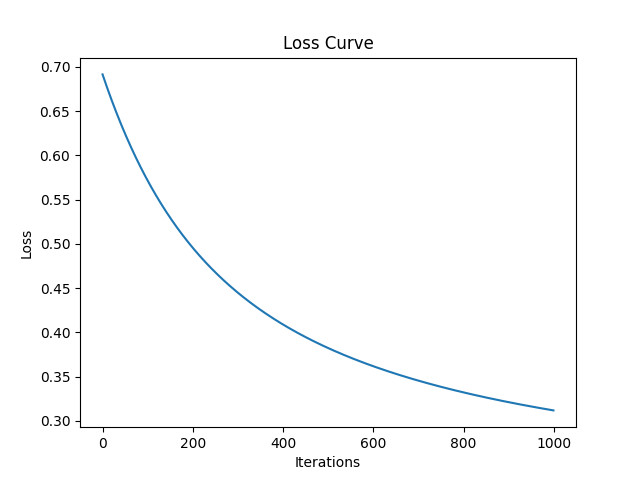
第二张图中我们绘制损失曲线，根据我们存放各训练中损失函数的列表即可绘制。

最后我们将预测和实际标签比对，可知分类准确率。

三、实验结果及分析

1.实验结果展示示例

image-20230516193943405

image-20230516193950451

1
分类准确率为:0.90

第一幅图为分类图，可以看到分类界限的两边几乎都是各自分类的点，只有分类界限附近的点有几个有混乱，可知分类效果较好。

第二幅图为损失函数图，可以看到在1000次训练中，我们的损失函数快速下降。

同时我们也通过直接输出看到了分类准确率在90%左右，达到了较好的分类效果。

四、思考题

本次实验中无思考题。

五、参考资料

① week13 神经网络v2 —— Our Class

② ML23-3 —— Our Class